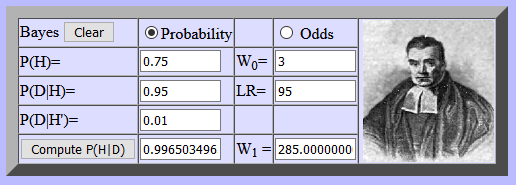
Source: Bayesian calculator at http://psych.fullerton.edu/mbirnbaum/bayes/BayesCalc.htm
What’s new?
Researchers at NIST have developed synthetic COVID-19 material which can be made with specific concentrations of the disease and which can be safely handled. This material can be used to determine the sensitivity of tests for COVID-19: how well does the test detect the presence of COVID-19 at different concentrations?
What does it mean?
For many years I taught university courses on probability and decision analysis. The mathematics behind COVID-19 testing is, of course, Bayes’s theorem, and that piece of mathematics is an insightful way of looking at medical diagnosis and public health decision making. Here is an example.
If a physician thinks a patient has a particular disease and gives a test to the patient, three numbers are necessary to determine the meaning of the test outcome for that patient. Let’s assume that, based on observations of the patient’s symptoms and before having the test administered, the physican thinks there is a 75% chance the patient has the disease; that is the first number. The test itself is described by two other numbers. The sensitivity of a test is the probability the test gives a positive result (that is, says the patient does have the disease) when the patient actually has the disease; we want that number to be high and let’s assume our test has a sensitivity of 95%. Specificity is the probability the test gives a negative result when the patient actually does not have the disease; we want that number to be high and let’s assume our test has a specificity of 99%.
Think of sensitivity and specificity by considering a person you suspect to have green/red color blindness. How well that person detects the colors is described by the person’s ability to say “green” when presented with an object that is actually green and the person’s ability to say “red” when presented with an object that is actually red. How well does the person detect the real color? How well does the test detect the true health status of the patient? Note that a person who always says “green” (whether shown a green or red object) and a medical test that always says “disease” (whether the disease is actually present or not) has perfect sensitivity (100%) but perfectly awful specificity (0%). A good test has high numbers for both sensitivity and specificity.
In my example, I write three statements shown in the three bullets below, using the notation “disease” (in quote marks) to indicate that the test says the patient has the disease. Note that the event “disease” (the test says the patient has the disease) is not the same as the event disease (the patient actually has the disease).
- P(disease) = 0.75, which implies that P(no disease) =0.25
- Sensitivity: P(“disease”|disease) = 0.95, which implies that P(“no disease”|disease) = 0.05. The first notation is read as the probability the test says the patient has the disease (“disease”), given the patient does actually have the disease (disease).
- Specificity: P(“no disease”|no disease) = 0.99 which implies that P(“disease”|no disease) = 0.01
The calculation using Bayes’s theorem is:
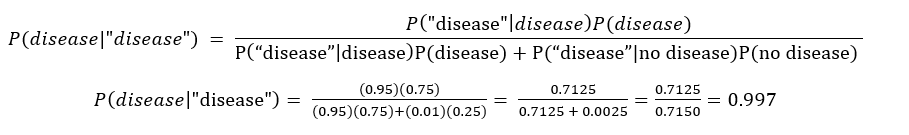
Thus, if the test says the patient has the disease, the physician is now almost sure (99.7%) that the patient has the disease. A similar calculation shows that if the test says the patient does not have the disease, the physician is then almost sure (99.0%) that the patient does not have the disease.
If 10,000 patients like this patient take the test, the results, on average, are:
| “Disease” | “No disease” | Totals | |
| Disease | 7125 | 375 | 7500 |
| No disease | 25 | 2475 | 2500 |
| Totals | 7150 | 2850 | 10000 |
Of the 10,000, 7125 will be correctly identified as having the disease, while 25 will receive a false positive, that is, they will be told they have the disease when they actually don’t. Another 2475 will be correctly told they do not have the disease, but 375 will receive a false negative, that is they will be told they don’t have the disease when the actually do have it.
I love math. I want to show you many more examples (with graphs!) because Bayes’s theorem is an amazing piece of math. But more than my love of the math itself, I love the usefulness of math so I will move on to the useful implications.
I have used Bayes’s theorem to model the thinking of immunohematologists (how do the results of blood tests revise beliefs concerning the antibodies present in a patient’s blood), geologists (how do test results revise beliefs concerning the likelihood of seismic activity in an area proposed for storage of nuclear waste), and insurance agent managers (how does the behavior of insurance agents revise beliefs concerning their loyalty to the insurance company).
However beautiful and useful the math in revising beliefs, the most important perspective to remember is that beliefs drive actions. What blood should the immunohematologist recommend for transfusion into the patient, where should nuclear waste be stored, and what action should a company take concerning an agent’s disloyalty?
With COVID-19 tests, action is complicated. Because of the lag in getting test results in many parts of the country and because of poor or unknown specificity and sensitivity of COVID-19 test results, a person cannot use the results to guide immediate action, nor can contact tracers use the results to know whose contacts to trace, nor can policy makers use the results to decide what public health measures should be taken.
What does it mean for you?
Bayes’s theorem is a way to think about revising one’s beliefs. One starts with prior beliefs, that is, initial beliefs about the presence of some factor (the disease or the market attractiveness of a new product) based on current information. Then, in the face of new information (a medical test or a test of the new product in one market), one needs to revise one’s beliefs.
That revision should be based on the ability of that test to detect the factor: if the factor really is present, can the test detect it and if the factor really is not present, can the test detect that? Is the test market a good indication of whether the product will be successful in other markets? The test is evaluated by its ability to detect reality. We want a test with 100% sensitivity and 100% specificity but, unfortunately, with some diseases (for example, Alzheimer’s disease), the only perfect test is an autopsy. I used to live in Columbus, Ohio, which, I was told, was an excellent test market for fast food items: if a product was a success there, it would succeed nationally and if it failed there, it would fail nationally.
Whenever there is uncertainty (that is, all the time), you won’t always be right. Any test has false positives and false negatives. That statement means the quality of a decision can only be judged by whether it was a good decision at the time it was made, not by whether it had good outcomes or not.
Beliefs drive actions, but a decision about actions must also consider the possible consequences of actions. With a different set of three numbers, the Bayes’s theorem calculation may leave a physician unsure whether or not the patient has a disease, but the physician may choose to administer a treatment anyway if early treatment is known to have an excellent outcome while lack of treatment often results in death.
One action leads to a series of actions. In decision analysis, we use a decision tree to represent a series of chance events and decision points into the future. A physician may try a treatment and then, depending on the patient’s results, continue that treatment or try a different one. Taking one action now may leave available later actions as options; a different action now may close off other later actions.
I taught an entire course (actually two entire courses) on decision analysis, But this piece is already longer than my usual writing. I would love to go on and on, but I will stop here: decision analysis is a very useful framework with many insights to offer decision makers.
Where can you learn more?
Regarding the formation of possessives, I come down on the side of Bayes’s theorem not Bayes’ but that dispute rages on.
Several calculators for Bayes’s theorem are available: here, here, and here. This one allows for more than two hypotheses (disease and no disease) and more than two test outcomes (“disease” and “no disease”).
Bayesian methods are increasingly used in sophisticated AI methods; see this example in machine learning.
Decision analysis software can help in modeling decisions. TreeAge is my favorite.
There are many books that serve as good introductions to decision analysis: Handbook of Decisions Analysis, Introduction to Decision Analysis by David C Skinner, and Choices by Michael D. Resnik. My favorite is still the 1968 classic by Howard Raiffa.
The American Academy of Family Physicians provides this overview of COVID-19 testing. This article discusses the sensitivity and specificity of COVID-19 tests for COVID-19 antibodies (not for the COVID-19 virus).