Jane M Fraser

Source: Wikimedia. This image is in the public domain.

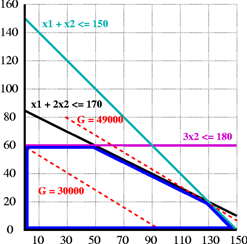
An illustration of a mathematical optimization problem with two decision variables (shown on the horizontal and vertical axes), three constraints (shown in black, teal, and purple), and a linear objective function (shown in red) that is to be maximized. The optimal solution is 130 for the variable on the horizontal axis and 20 for the variable on the vertical axis; that solution yields a value of 49,000 for the objective function.

What’s new?

As reported by Nature and phys.org, the 2021 Abel prize was awarded to mathematicians László Lovász and Avi Wigderson for their work on computational complexity.

What does it mean?

If, like me, you enjoy putting together jigsaw puzzles, you know that every puzzle is labeled with an important number: the number of pieces. That number is a fairly good predictor of how much time it will take you to put together the puzzle. Once the puzzle is done, you know you have solved it correctly simply by seeing that the resulting picture is complete. You have found the unique, best solution.

Much of what computers do takes the form of solving mathematical puzzles: finding the best route for a delivery van, assigning flight crew members to flights in the best way, assigning jobs to machines in a production facility, deciding on the best way to cut a tree trunk into lumber, and so forth. For many mathematical puzzles, like the jigsaw puzzle, the size of the puzzle is a fairly good predictor of how long the puzzle will take to solve, and for some – but not all such mathematical puzzles – when you have found the best answer, you can easily confirm that the answer is the best.

The field that deals with solving mathematical puzzles like these is called optimization (notice the use of the word “best” in each of the stated puzzles above) and the field that studies the difficulty of such puzzles (how long will the puzzle take to solve) is called computational complexity.

In optimization, the puzzles we solve are expressed in mathematical form. We want to select values of decision variables to maximize or minimize an objective function (expressed as a function of the decision variables) while meeting all of the constraints of the problem (expressed as inequalities or equations, again as functions of the decision variables). In my June 27, 2020, blog on operations research I wrote about linear programming as an example, where the objective function and constraints are all linear functions of the decision variables, but other puzzles we want to solve may not be linear. Also, in some puzzles, the values of the decision variables are restricted to be integers (that is, numbers with no decimal part): you can’t assign 0.8 of a crew member to a flight, for example.

Computers solve these problems by using algorithms: an algorithm tells the computer program exactly what to do and the computer chunks away and eventually tells you the best solution to the problem. The issue is how long it will take the computer to find the best solution, and in some cases the answer is disappointing: more time than the total time so far in the universe. Imagine a jigsaw so big that it would take almost forever to complete. In such cases, we may need to use a heuristic, which is a method that can get us an answer to such problems that may not be the best answer, but that we know it is a good answer.

In some puzzles, when you have found the best answer, you can easily confirm that the answer is the best. If, by luck, you pick up a jigsaw puzzle piece and it clicks into place, you know you are correct. With some mathematical puzzles, introducing randomness into the heuristic can speed up the process of finding a good, even best answer.

As the Nature article on the Abel prize says: “But since the advent of computers in the twentieth century, the emphasis in research has changed from ‘can an algorithm solve this problem?’ to ‘can an algorithm, at least in principle, solve this problem on an actual computer and in a reasonable time?’”

The winners of the Abel prize contributed to the solution of mathematical puzzles and to the field of computational complexity. Lovász has contributed to the solution of mathematical puzzles that can be expressed as movement on a network, seeking the best solution. Wigderson’s contributions relate to the use of randomness in finding solutions and relate to so-called zero-knowledge proofs, a way of proving that a puzzle has been solved without actually revealing the solution.

What does it mean for you?

Computers do more and more for us every day (just take a look at your cell phone), often relying on algorithms and heuristics to solve mathematical puzzles. We want them to solve bigger and bigger problems, so the answer is always, get a faster or bigger computer, but computational complexity helps the designers of algorithms know when a faster computer is likely to be successful and when the problems are simply too big to tackle. The results of computational complexity are important in guiding this work.

Paradoxically, sometimes we want to design problems that will take an enormous amount of time to solve; that idea forms the basis for most computer security. Guessing your 16-character password is beyond the reach of most computers. Complexity theory underlies cybersecurity and encryption, the methods that are meant to keep your information safe from attack. It also forms the computational basis of crypto currencies such as Bitcoin.

Where can you learn more?

The Britannica article on optimization is a nice introduction to the field, including some history. This article from Forbes discusses the types of business problems that can be solved by mathematical optimization. The professional organization INFORMS is one of several for professionals in optimization and computational complexity; they have an excellent history of mathematical optimization here.

This work is licensed under a Creative Commons Attribution 4.0 International License.